|
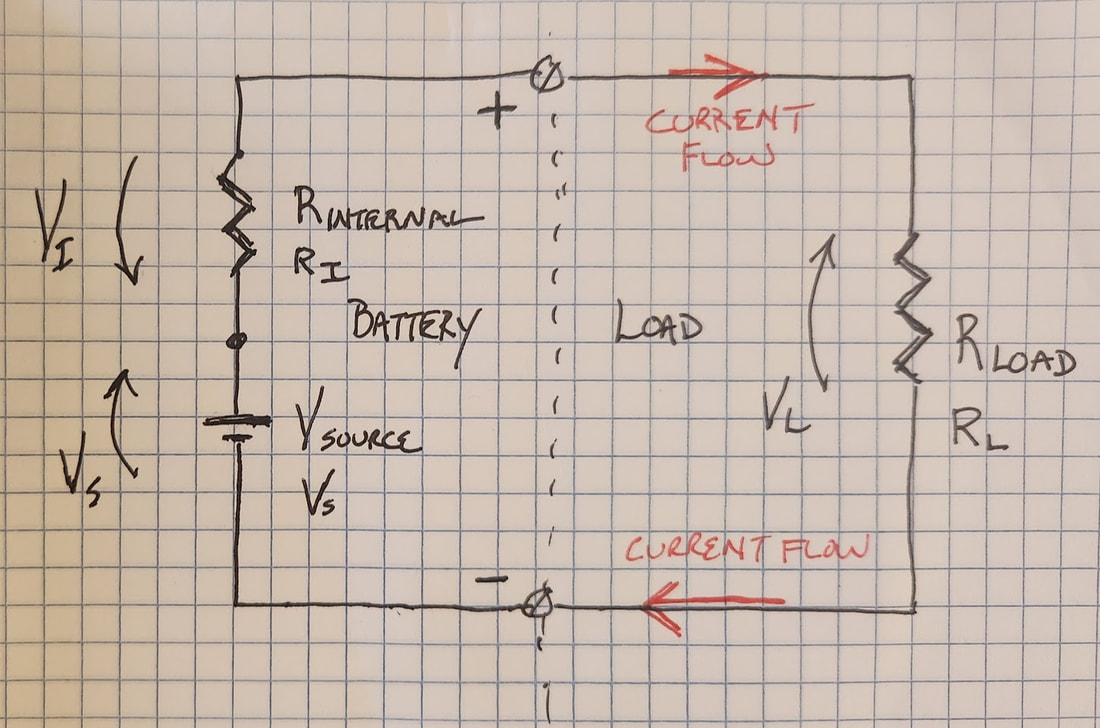
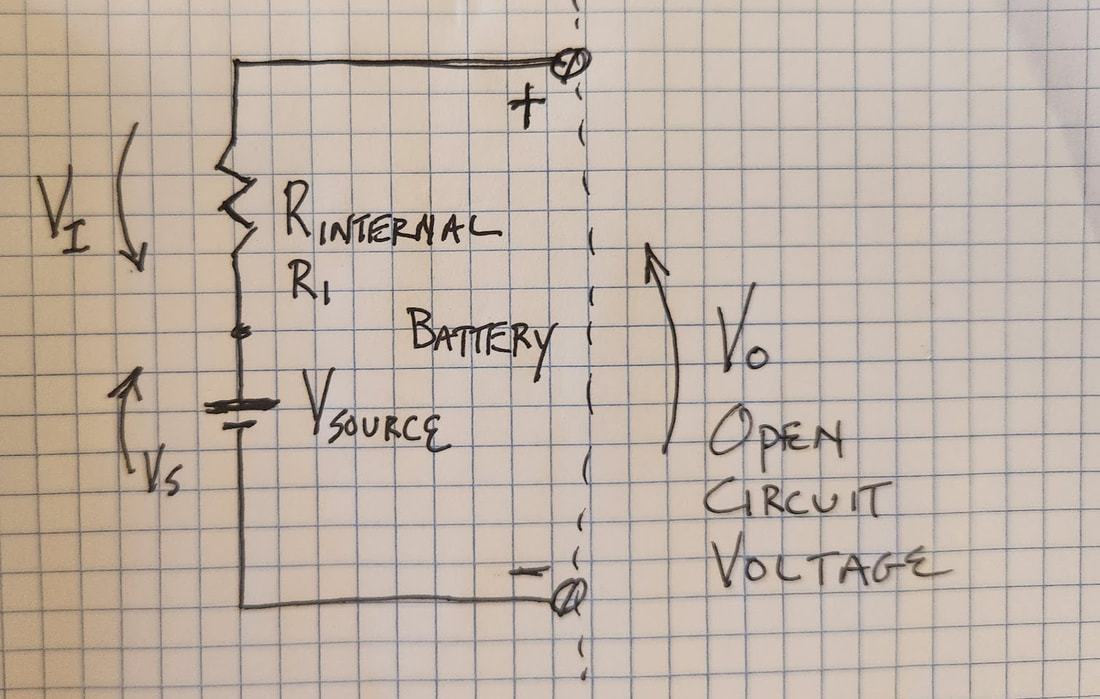
It would seem the obvious answer would be "Get a voltmeter and test it." Sadly, that doesn't really work. A quick voltage test can be very deceptive. Unless you get more data, you are about as likely to draw a bad conclusion as a good one. A good battery can give a lousy voltage reading simply because it needs to be recharged. But a bad battery can show a perfectly good voltage, but completely fail to turn your starter motor. How can this be?! Welcome to WrenchMonster's basic course on electricity. Let's start with an analogy. Electricity is like water. It has pressure (voltage) and volume (amperage). Everybody knows about voltage. High voltage is dangerous. Touching a high voltage wire hurts and might kill you. But the volume aspect is not obvious because we cannot see electrons. Amperage, the volume feature of electricity, relates to the number (volume) of electrons that are going through the wire. A voltage measurement tells us how hard the electrons are being pushed. An amperage measurement tells us how many electrons are going through the wire. It is easy to imagine a water hose with giant pressure behind it...and a sprayer nozzle on the end of the hose that is just a pinhole, so only a tiny amount of water actually comes out. It may come out hard and fast, but if you point it at a heavy object, it probably won't knock it over. On the other hand, if you have a fireman's hose, which is very fat and can carry lots of water...and it has a nozzle on the end that is MUCH larger than a pinhole, you can bet turning that hose onto a heavy object (say a cement block sitting on the sidewalk) will knock that concrete block and roll it down the street...even if the pressure behind that water is no higher than is behind your household tap water (which is exactly the case for all the fire hydrants that line our streets because they are fed by the same water mains that are connected to our houses). Electricity works the same way. Volume matters, whether it is gallons per second of flow or electrons per second of flow. When measuring electrical circuits, we need to know about voltage, amperage and RESISTANCE (how much the flow is being held back). The size of the nozzle at the end of the hose does matter. We need to know how hard it is for the electrons to get through the circuit. There are lots of ways to resist the flow of electrons. A switch breaks the circuit entirely, like a valve cutting off the flow of water. The voltage, the pressure, is still there, but the resistance is nearly infinite, so the flow of electrons (measured in amps) goes to zero. But it is also possible to throttle the flow of electrons; to open the valve a little bit. Different materials have different resistance properties. Copper has very low resistance. That's why so much of our wire is made of copper. Carbon can pass electricity, but not very well, so we can use chunks of carbon with wires connected to each side to intentionally hold back the flow of electrons. If you've ever looked at a PC board in a computer you've seen lots of these devices, which naturally are called "resistors". And it's also true that other chemical compounds may be better or worse at passing current...including the chemical compounds in batteries. What's more, how easily the chemicals in a battery can pass current CHANGES as the battery ages...and that begins to answer the title question. The proper way to test a battery is to measure the internal resistance of the battery. Unfortunately, you can't simply set your meter to OHMS (the scale we use to describe how much something resists the flow of electricity) and connect it to the battery. All that will do is blow the meter protection fuse in the meter...or burn up the meter if it doesn't have an internal fuse. To figure out the internal resistance of a battery we need to measure other things and then use some math. Ohm's Law: Volts = Amps x Ohms which is also written in electrical shorthand as V = I x R Yes, there was a Mr. Ohm who figured out this math. And because of the magic of algebra, we can express Ohm's Law three different ways... V = I x R I = V / R R = V / I V means Volts, R means Resistance (measured in Ohms) and, I (a capital "i") means Current (measured in Amps). Therefore, any time we know two things about electricity flowing through something, we can calculate the third one. To figure out the internal resistance of a battery, which we cannot measure directly, we need to measure the things we can measure, and then use math to calculate the internal resistance of the battery. One of the most important things we need to measure along the way is the voltage the battery can hold across a known load (a resistor of known resistance that’s connected to the battery terminals). Because of the work of another smart guy, Gustav Kirchhoff, we know how electricity works in a complete circuit. In a series circuit (one where the electricity flows in a single loop from the battery, to a load resistance, and back...without branching off and going elsewhere) we know that any push caused by the battery is balanced exactly by the push back offered by the elements in the circuit. So, if a “push” is a rise in voltage, then the “push back” is a drop in voltage. In a series circuit, for every rise in voltage as we go around the loop, in the end, when we get back to where we started, there must have been exactly the same amount of voltage “drop” (a loss of electrical pressure) by the time we get back where we started. Or to put it another way, all the rises and drops (which we express as a negative number) in voltages in a series circuit add up to zero. We also know the current flowing in one part of a series circuit must be exactly the same in every other part of the circuit, just like if we had a loop of hose connected to a water pump. All the water being pumped into the hose would circulate back to the intake of the pump. As long as our hose has no leaks, the amount of water in the loop of hose never changes…it just goes around and around. Same for electricity... This is a picture of a typical circuit diagram. Nothing special. A zig-zag symbol represents a resistor or the resistance of an object in the circuit. The parallel lines (Vs) represent the "electron pump" inside the battery; the combined effect of all the battery chemistry in the battery that causes the push on the electrons that we measure as voltage. The screw terminals marked with (+) and (-) represent the external terminals of the battery. The whole point of this article is Ri, which is shown between the positive terminal of the battery and the voltage source inside the battery. That symbol represents the total internal resistance of the battery, which we model mathematically as if it was a single resistor inside the battery. Naturally, it’s not actually as single resistor inside the battery. Internal resistance is the net effect of all the resistive mechanisms at work inside the battery, just like Vs is net effect of the battery chemistry trying to push current out of the battery. We lump those push and resistance effects into these two circuit elements mathematically to simplify the calculations we need to do. (And it really works!) The voltages in this diagram are marked as Vs (the Source Voltage), VL (the voltage drop across the load resistor connected to the battery terminals), and Vi (the voltage drop across the internal resistance inside the battery). FYI - The arrowheads convey where the voltage is higher, meaning if you were able to connect a voltmeter at the dot between Vs and Ri, you would see a higher voltage at the dot than at the other end of Ri...or to put it another way, if you walk from the negative terminal of the battery, clockwise around the circuit, voltage would be the highest at top of Vs, would drop as you crossed Ri and would drop further as you crossed RL. That is what we mean when we talk about Kirchhoff's Voltage Law (the voltage rises and drops in a series circuit must sum to zero). We express voltage drops in an equation as a negative number so, Vs - Vi - VL = 0. In a series circuit, if we measure the voltage across the load resistor, and if we know the resistance of the load resistor, we can calculate the number of amps of current that are flowing through that resistor. And because this is a series circuit and no electricity is leaking out to other places, we know that same number of amps are flowing through the battery too. If we know the value of Vs, VL, and we know how much current is flowing through the battery while the load is connected, we can calculate the internal resistance of the battery. But how do we measure the internal “push” of the battery? How do we measure Vs? The test setup to measure the Vs of the battery is shown in this next diagram. It is the battery sitting by itself with nothing connected to the terminals. The voltage the battery can produce with nothing connected is known as Open Circuit Voltage, or the No-Load Voltage of the battery. If there’s nothing connected to the battery, we know there’s no current flowing through the battery...and that means no current is flowing through the internal resistance of the battery. Because V = I x R, we can be sure that if the I term, amperage, in the equation is zero, no matter what the value of R, zero times R is always zero. So, if the battery can produce Vs (source voltage) internally, and none of it is being dissipated across Ri, meaning Vi must equal zero, then what we can see at the output terminals of the battery, Vo, must be equal to Vs. Which is to say, we can actually measure the value of Vs directly at the terminals of the battery, as long as we don't connect anything to the battery. Nothing to it, right? Except we need to connect something to the battery to measure its voltage. Here's the good news. Voltmeters are specifically designed to present a VERY high resistance to any circuit they touch. The whole point is for the meter to leave the circuit under test undisturbed. The input resistance of most voltmeters is millions of ohms, which is about as close to electrically invisible as you can get. The current that goes into our voltmeter is so small we can ignore it in our calculations. So, at the top of this article I said just connecting your voltmeter to your battery would give you the wrong answer...and that is true, depending on what answer you are trying to get. If you want to know the Vs of the battery, it’s exactly the right thing to do. But the Vs of the battery is only part of the story. What we really want to know is "What voltage can the battery maintain with an actual load hooked up?"...like the starter motor for example. And that’s where the value of Ri becomes so critical. Have you ever seen a bike or a car that has all the lights come on when you turn it on, but they all go dim or out when you hit the starter? Your lights do not require very much current to light up, maybe one or two amps of current. LED lights need even less. A bad battery (or a poorly connected battery) is able to produce enough voltage, under that light load, to make things work. But as soon as you put a heavy current demand on the battery, 100 amps or perhaps more, by connecting something like the starter motor, the output voltage of the battery collapses; the starter motor will not run and the lights go dim. That is all because of the Ri, the internal resistance, of the battery. Let's suppose for the moment that your starter motor requires about 10 volts and 100 amps of current to spin with conviction (those are not unreasonable numbers for a motorcycle starter motor). We know that if the motor (RL) is pulling 100 amps, then 100 amps must be flowing through the battery too, including Ri, the internal resistance of the battery. Let's say the battery we are using shows 12.6V of open circuit voltage, which we now know means the value of the battery's Vs is 12.6V. If a starter needs 10 volts at 100 amps, then the internal resistance of the battery must not use more than 2.6V when the starter is connected for us to get a goods spin from the motor. We now have all the data we need to calculate the how much resistance Ri can have before the voltage left for the starter motor falls below acceptable limits. 2.6V / 100 A = 0.026 ohms, otherwise known as 26 milliohms or 26 thousandths of an ohm...and that’s not much. But in this example, where we are trying to spin a 100A starter, it is as high as the internal resistance of this battery can get and still produce the voltage and current needed for this starter motor. In this example it is low enough to spin that starter properly, but if the internal resistance goes any higher, the voltage it dissipates will go higher and the output of the battery will drop below 10V, starving the starter motor of the power it needs. But suppose the Ri of that same battery was 0.100 ohms...only 4 times higher. In that case, a 100A demand on the battery would result in an internal voltage drop across the internal resistance of the battery of...100 amps x 0.1 ohms = 10 Volts. That means 10 volts of the 12.6 volts that battery can produce are stuck inside the battery and we would only see 2.6 volts on the output terminals of the battery. That, my friend, is a very bad battery. So that is why Ri matters and how an Ri that is too high can make what may look like a good battery with a simple voltmeter test, proves to be completely useless when it comes to starting your machine. But we need to get back to the original question: "How can I tell if my battery is good?". The answer is a two-step process: 1. Test it with no load; nothing connected but the voltmeter and record Vs. 2. Test it again with a load of known value; a test load, and record VL. To get valid results, it is best to use a pretty heavy test load, so the battery is really having to push some current when it is under test. That’s the idea behind the big clunky battery testers sold at the auto parts stores, like this one, for example.
Ok, back to the problem at hand. We have a voltmeter and now we have a test load of known value. We are ready to figure out the internal resistance of our battery. Let's review the whole process from the start... 1. We measure the Open Circuit Voltage of our battery, which we know is equal to the Vs of the battery...and let's say we measure 12.6 Volts. 2. We measure the resistance of our test load, and find we have a 0.5 Ohm resistor inside the tester. 3. Now, we connect the test load to the battery (not for too long...20 seconds or so) and we measure the voltage on the battery terminals WHILE THE LOAD IS CONNECTED, and let's say we read 12.4 Volts on our voltmeter. 4. Now we have all the data we need and we can do some math. Vs is 12.6V and the voltage measured across the load, VL, is 12.4V, so the missing 0.2V must be across the only other element in the circuit, which is Ri, the internal resistance of the battery. The equation for that is Vs - VL = Vi = 0.2V (so says Mr. Kirchhoff). We know the load resistor has a value of 0.5 Ohms and the voltage across the load is 12.4V while connected to the battery, so the current flowing through the circuit (which is the same through all components in the circuit, including the internal resistance of the battery) while the test load is connected is VL / RL = Test Load Current = IL, which in this case is... IL = 12.4V / 0.5 Ohms = 24 Amps And with that, at last, we have the last piece of the puzzle we need to figure out internal resistance, Ri... Ri = Vi / IL = 0.2V / 24A = 0.0083 Ohms But...is that good or not? It depends on what the Ri of the battery was when the battery was new. A little more math allows us to figure that out. Each battery has a CCA rating (CCA = Cold Cranking Amps). It’s a rough indication of how much current the battery is designed to produce in cold weather, while maintaining an output voltage of about 7 volts (when it’s hard for batteries to deliver power). Car batteries usually promise hundreds of Amps in freezing weather, but motorcycle batteries are smaller and normally deliver less, typically 100 to 200 CCA. Let's say the one we have been testing in this example has "120 CCA" stamped on the outside. Because we’re probably not going to put the battery in the freezer overnight before we test it, it’s going to be hard to compare our test results to the battery CCA spec, but it’s safe to say we can consider the CCA rating of the battery an absolute minimum amperage we should expect to see from a battery while sitting our garage on a spring day...and here is the key...the CCA rating of the battery, more or less, is the minimum amperage we should see when the battery is producing at least 10V at "room temperature" on the output terminals. Note: Different standards organizations have slightly different test procedures for testing the CCA of a battery, but they are all pretty similar to each other...and close enough that we can ignore those differences in this discussion. The reason I cite 10V at room temperature vs. 7.2V at -18 degrees C (one of the CCA test standards) here is that the battery should perform 20% - 30% better at warmer temperatures...and it’s a good ballpark number for the least voltage we want to see on our starter motor when we’re trying to start the bike, and therefore a good cutoff voltage for evaluating whether the battery is minimally acceptable. Because your bike's designers selected a battery with a certain CCA rating, if we use it as our guide, we know we have scaled out expectations for the battery to roughly fit the needs of our bike. If we expected output current performance that matched a car battery, every motorcycle battery would look bad. (And that is why the good/bad scale on that cheap battery load tester we cited earlier may not be valid for testing your motorcycle battery.) Because there is no practical way to load a battery down in the shop so that it produces exactly 10V, we go back to using math... Again, we still know Vs of our battery is 12.6V. If we – hypothetically - load this battery down so hard that it can only produce 10V on the output terminals, how much current must it be producing at the time? We already have all the data we need to figure that out... If Vsource is 12.6V and the hypothetical Vload is 10V, the voltage across the internal resistance of the battery in that case would be 2.6V. We already figured out internal resistance is 0.0083 Ohms. In that situation, how much current must be flowing through the internal resistance of the battery? 2.6V / 0.0083 Ohms = 313.25 Amps! Wowzer! That is WAY more than the 120 Amps the sticker on the battery says it must be able to produce. Awesome. The Ri of this battery is much lower that is needs to be to meet the 120 CCA spec. This is a very good battery. What might a "bad" battery look like? Suppose we had that same 120 CCA battery, but it showed a Vs of 12.3V when we did out open circuit voltage test, and after we did know-load testing, we did our math and figured out it has an internal resistance of 0.0250 ohms. We can do the math for the hypothetical load with these numbers the same way we did before... Voltage across the Internal Resistance = 12.3Vsource - 10Vload = Vi = 2.3V then, 2.3Vinternal / 0.025 ohms internal resistance = 92 Amps Bummer. that’s not so great for a battery that’s supposed to have a 120 CCA capability, particularly since we didn’t do our testing under the freezing conditions of a real CCA test (which would have resulted in us measuring an even higher internal resistance, causing an even worse current output when the battery is loaded down to 10V). Even though we proved this battery can ALMOST get to its rated 120A @ 10V output spec, it did not make it, even in warm test conditions. This battery has got to go. So that's the story. You can test your battery. Yes, you do need a voltmeter, but that’s not enough. You also need a known-value test load and some math skills. Or you can buy a battery tester that actually does all that work for you and tells you the internal resistance of your battery when it is done. Something like this one... This little tester is made by Ancel. It, and similar units from other vendors, can be purchased for less than $40. You tell the tester the model number of the battery you're testing (or the CCA of the battery you’re testing) and it does the testing and the math for you. It tells you the internal resistance of the battery and gives you a broad assessment of the battery's "State of Health" or SOH.
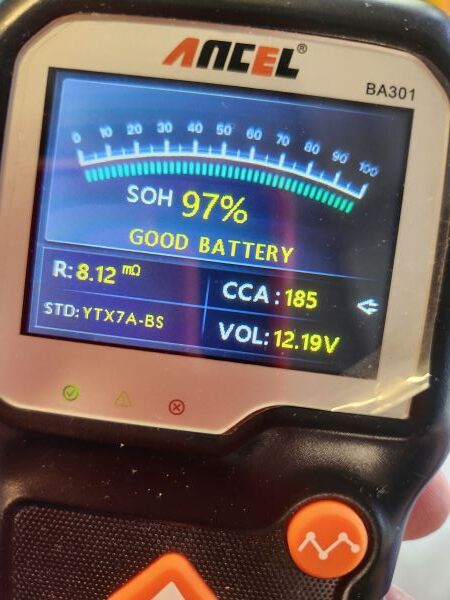
This picture shows an Ancel BA301 tester connected to a battery for testing. The battery is currently showing an Open Circuit Voltage of 12.19V (In this case they are calling it Open Loop Voltage, shown on the display as "VOL") and the measured Internal Resistance of the battery is shown as "R: 8.12 mohms (i.e. 0.00812 ohms or 8.12 milliohms). And the display shows that the tester evaluated on the basis of it being rated for 185 CCA (Recall our earlier discussion about CCA. If we had told the tester the battery under test is rated for 600 CCA, despite measuring the same 12.19V VOL and 8.12 mohm Ri, the tester would say we have a bad battery.) Pretty cool, huh? By the way, this battery should be recharged to see if it will come up to 12.4V to 12.6V. If it does, it will probably show an even better internal resistance. The moral to that story is that you can’t expect to get reliable test results from a discharged battery. To do a good test, charge it up, use it for a few seconds (hit it with a test load, or hit the starter button for a sec, or turn on the headlights for 10 seconds) to burn off the deceptive “surface charge” and then do your testing. Comments are closed.
|
Categories
All
Archives
January 2024
|
|
© WrenchMonster 2018
|
WrenchMonster™ is a Division of DemonLite, LLC.
|


 RSS Feed
RSS Feed